Importance of low distortion

When talking about the distortion of audio electronics such as a DAC or a power amplifier, low order harmonics, particularly 2nd and 3rd, are often considered "harmonious" and "benign". In contrast, high order harmonics, which are not harmonically related to the fundamental tone, are considered noxious. This argument usually supports the idea that tube amps sound better, because tubes only add low order distortion, or that low- or zero-feedback amplifiers sound better because feedback adds higher order harmonics.

Let's conduct a little experiment. Let's say we test an amplifier that adds 0.01% of the 2nd harmonic (H2) and 0.001% of the 3rd (H3):

The distortion is not particularly high and is all low order, harmonious and benign, perhaps even euphonic.

Now let's play a simple chord, A-C#-E:

Oops. In addition to H2 and H3, our benign test amplifier sputters a bunch of intermodulation products, musically unrelated to the chord, with levels comparable or in some cases above those of H2 and H3. These are not euphonic and would not be masked by music. Worse, they will mask the music itself.

So, an amplifier with low order and relatively low level, "benign" distortion may be euphonic with a single tone but not so euphonic with a chord. Practically speaking, such an amplifier would have genre preferences: it might sound fantastic on simple music such as solo vocal, but would get confused with anything moderately complex, and it would mush a full orchestra or, say, a Rammstein recording.

Current Dumping: Fine Print

This post is a part of the series on audio amplifier feedback. The contents of the series can be found here.

In the previous post, I explained how current dumping works on an intuitive, qualitative level. Let's go into the next level of detail.

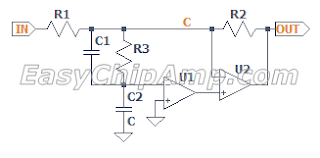
A current dumping amplifier is a feedback amplifier consisting of a low distortion, low power amplifier A and a high-power, distorting buffer ("current dumper", here Tr1 and Tr2)  inside a common negative feedback loop:

Negative feedback reduces, but not completely eliminates, the distortion that the current dumper adds to the signal. From my earlier post, the share of that distortion that remains at the output (point D at the schematic above) after the negative feedback is applied is given by the Error Transfer Function $${ETF={1 \over {1- A \times B}}}$$ where $A$ is the transfer function (basically, the frequency-dependent gain) of the integrator composed of A,R1,C1, and $B$ is the transfer function of the feedback network. In this case, the feedback network has unity gain and is connected to the inverting input of the integrator, so $B=-1$, and $${ETF={1 \over {1+ A}}}$$ Therefore of the total open loop distortion $\epsilon$ of the current dumper, at point D we observe $$\epsilon _D={\epsilon \times ETF}=\epsilon {1 \over {1+ A}}$$ Since the current dumper adds distortion $\epsilon$, for this to happen, the input of the current dumper (point A at the schematic above) should see "pre-distortion" $$ \epsilon _A = {\epsilon_D - \epsilon}={{\epsilon {1\over {1+ A}}}-\epsilon}=-\epsilon{A \over {1+ A}}$$ At the load, $\epsilon_A$ and $\epsilon_D$ combine in reverse proportion to the impedances of R2 and L1: $$\epsilon_{LOAD}\propto {\epsilon_A Z_{L_1} + \epsilon_D Z_{R_2}}$$ Note that the load impedance affects the absolute level of the combined signal at the load but not the proportion of $\epsilon_A$ to $\epsilon_D$.

Combining the last three equations and dropping the common denominator $1+A$: $$\epsilon_{LOAD}\propto {\epsilon (Z_{R_2} - A  Z_{L_1})}$$

Clearly, the perfect cancellation of the current dumper's distortion occurs when $$Z_{R_2} = A  Z_{L_1}$$

For the implementation above, under ideal conditions, $Z_{R_2}= {R_2}$, $Z_{L_1}= s {L_1}$, $A=1/{(s R_1 C_1)}$, and the perfect cancellation means

$$R_2={L_1 \over {R_1 C_1}}$$

which is the result from [1]: "For the linearity of Tr1 and Tr2 to be immaterial then L must equal RRC".

However, by going through the algebra above, we obtained a more general and quite remarkable result: a perfect distortion cancellation requires the ratio of $Z_{R_2} /  Z_{L_1}$ to mimic the amplifier's loop gain $A$. This gives us the freedom to make current dumping work under less than ideal conditions, as well as in different implementations than Walker's.

For example, the gain of an ideal integrator $A=1/{(s R_1 C_1)}$ is infinite at DC, which is practically impossible. A more realistic integrator has a transfer function $A=A_0/{(1+s{T_p})}$, where $A_0$ is the finite DC gain and $T_p$ is the time constant corresponding to the integrator's single pole. Substituting this into our perfect cancellation condition $Z_{R_2} = A  Z_{L_1}$, we obtain $${Z_{L_1}} = {R_2 \over A} = {R_2 \over A_0}{ (1+s{T_p})} = {R_2 \over A_0}+s {R_2 T_p \over A_0}$$

Since the impedance of a realistic inductor is $$Z_L=R_{ser}+sL$$where $Rser$ is the DC resistance and $L$ is the inductance, it is clear that ${R_2 T_p / A_0}$ corresponds to the inductance, and ${R_2/A_0}$, to the DC resistance of the inductor providing a perfect distortion cancellation.

Since we have five variables $L_1$, $R_{ser}$, $R_2$, $A_0$, $T_p$ and two equations $L_1={R_2 T_p / A_0}$ and $R_{ser}={R_2/A_0}$, any three variables can be chosen freely. Note that $A_0$ and $T_p$ together determine the unity-loop-gain frequency $F_0=A_0/(2 \pi T_p)$, which may be a more meaningful parameter.

Finally, let's make a quick reality check and see if the ideal distortion cancellation in this example can still be implemented with reasonable parts. In my previous post, I found that a perfect cancellation is possible with a L=3.3μH inductor, R2=21ohm resistor and an amplifier with the unity-loop-gain frequency F0 of 1 MHz. With the DC gain of the amplifier at, say, 80dB (×10k), the DC resistance of the inductor should be 21/10k=2.1mOhm for a perfect low-frequency cancellation. This looks too low to be implemented in real hardware, esp. after the impedance of PCB traces, etc., is taken into account. One way to address this is to reduce the DC gain (and hence the loop gain at the frequencies below the amplifier's pole) while keeping the same unity-loop-gain frequency. Another would be to increase the unity-loop-gain frequency, which would require a proportional increase in R2 and Rser. However, practically speaking, the perfect cancellation at low frequencies may not be as important, as the amplifier has more loop gain there, and the feedback, rather than feedforward, will take care of the distortion of the output stage.

Stay tuned for an implementation of current dumping different from Walker's.

References

1. P. J. Walker and M. P. Albinson, "Current Dumping Audio Amplifier," presented at the 50th AES convention, March 1975.
2. S. Takahashi and S. Tanaka, “Design and Construction of a Feedforward Error Correction Amplifier,” JAES vol. 29, pp. 31-37, Jan/Feb 1981.

Current Dumping Revisited

This post is a part of the series on audio amplifier feedback. The contents of the series can be found here.

Current dumping is a way of constructing a power amplifier where a low-power, low-distortion amplifier is used to correct the distortion of a higher-power, but less linear, amplifier ("current dumper"). The underlying assumption is that it is easier to construct a low power, low distortion amplifier than a high power, low distortion amplifier.

Current dumping was introduced by quintessential English audio company Quad and was used in a series of Quad's power amplifiers starting with the Quad 405. Quad's founder, P. J. Walker, presented the concept at the 50th AES convention in 1975 [1].

There has been much interest and public discussion of current dumping in late 1970s and early 1980s. While most reviewers used more or less complicated math to explain why and how current dumping works, the basic implementation is easy to understand on an intuitive level.

The following schematic is from Walker's original AES paper:

Here, A is the low power, low distortion amplifier, and Tr1 and Tr2 form the "current dumper". The feedback for A is taken from the output of the current dumper. The load is connected to both A (via R2) and the current dumper (via L1). 

Any distortion appearing at the output of the current dumper Tr1 Tr2 (point D in the schematic) is fed to the load via two parallel branches:

• Via L1
• Via the integrator A R1 C1, followed by R2:

 

If these two branches feed the load with the distortion of equal amplitude and opposite in phase, the load will see zero distortion - this is the big promise of current dumping.

Intuitively, since L1's impedance increases with frequency at 20dB/decade, the distortion it feeds to the load falls with frequency at the same rate and lags in phase by 90°. The same distortion coming via the integrator also falls with frequency at 20dB/decade, has a 90° phase lag, and is inverted - that is, its the phase is opposite to the distortion coming via L1. Since the levels are proportional and phases are opposite, with the right choice of R2, the residual distortion from the current dumper can be nulled.

The circuit is particularly easy to analyze if the gain of A is assumed to be infinite. In this case, the inverting input of A (labeled F) is at the ground level (that is, zero distortion signal) due to the feedback via C1. If the distortion is nulled perfectly, the load (labeled L) is also at the ground level. The current via R1 is equal to that via C1, and the current via L1 is equal to that via R2. A little algebra quickly shows that this can only happen when the DC resistance of L1 is zero, and its inductance is L1=R1×R2×C1. In the language of the AES paper, "For the linearity of Tr1 and Tr2 to be immaterial then L must equal RRC".

It is worth nothing that the gain of the integrator A R1 C1 is the loop gain of the amplifier, and that R1×C1 is the time constant corresponding to the frequency where the loop gain becomes unity (in magnitude; a 90° phase lag remains). For a perfect distortion cancellation, the impedances of L1 and R2 at that frequency must be equal.

Let's make a reality check and see if the ideal distortion cancellation can be implemented with reasonable parts. A typical Miller-compensated audio amplifier behaves like an integrator A R1 C1 above and reaches the unity loop gain at the frequency of about 1 MHz (see my previous post for an explanation). 1MHz corresponds to R1×C1 of about 0.16 μS. (Walker's own values, shown on the schematic above, give the unity-loop-gain frequency of 4.8MHz, which I believe is rather optimistic with the parts that were available in 1975.)

A typical air core inductor of the type commonly found at the output of such an amplifier will have an inductance in the low single μH range, so let's use Walker's 3.3μH. With R1×C1=0.16 μS, the cancellation condition above gives us 21 ohm for the value of R2. If we want the whole current dumping amplifier deliver, say, 100W peak power (50W RMS on a sinewave) into a 8 ohm load, our low-power, low-distortion amplifier A would only need to provide about 140mW into R2 at 20kHz, and less at lower frequencies. That looks rather realistic.

What is unrealistic are the assumptions of infinite gain for A and a zero DC resistance for the inductor. Still, the cancellation condition can be generalized for a more realistic setup, but the details will have to wait for another post.

References:

1. P. J. Walker and M. P. Albinson, "Current Dumping Audio Amplifier," presented at the 50th AES convention, March 1975.
2. P. J. Walker “Current Dumping Audio Amplifier,” Wireless World, vol. 81, pp. 560-562, Dec. 1975.
   

Bootstrapped collector loads

This post is a part of the series on audio amplifier feedback. The contents of the series can be found here.

A bootstrapped collector load is a pair of resistors connected in series, with their common point actively driven, often by a unity gain buffer via a large capacitor:

Bootstrapped loads have been popular in audio amplifiers for more than 50 years, although these days they are largely replaced by constant current sources.

The work of a bootstrapped load is easily understood. Because of the unity gain buffer, the right side of the capacitor $C$ (see the schematic above) sees the same potential as the bottom end of $R_2$. As long as the voltage across the capacitor is relatively stable, the voltage across $R_2$ is relatively stable, and so is the transistor's collector current flowing through $R_2$. In particular, the collector current changes only a little with changes in the collector potential (e.g. an audio signal), as if the collector load resistance is large.

Quantitatively, it is obvious that at DC, $R_1+R_2$ is the only load that sets the quiescent collector voltage. To find out AC response, one needs to e.g. write down node equations, which reveal that a bootstrapped load presents a frequency dependent impedance of the form $$Z = (R_1 + R_2) \times (1+s T_z)$$

where $T_z = (R_1 || R_2) C$.

The impedance increases with frequency at 20dB/decade, as would the impedance of an inductor. Effectively, a bootstrapped load is a synthesized inductor with the series resistance $R_1+R_2$ and the inductance $L = R_1 R_2 C$. For example, with R1=R2=1kOhm and C=10uF, the equivalent inductance L=10H.

In a real circuit, this synthesized inductor is not the only collector load - connected in parallel to it are the output impedance of the transistor and the input impedance of the buffer. If this input and output impedances are lumped into Ri:

then the combined collector load has the form $$Z = {R_i || (R_1 + R_2)} \times {{(1+s T_z)} \over {(1+s T_p)}}$$ where $T_z = (R_1 || R_2) C$ as above and $T_p = {{ (R_1 + R_2) \over (R_i +R_1 + R_2) } C}$.

I will look more into the behavior and practical uses of a bootstrapped load in separate posts.

High Precision Composite Op-Amps, Part 5 - Cart Before Horse

 

This post is a part of the series on audio amplifier feedback. The contents of the series can be found here.

In my previous post on this topic, I gave a couple of practical examples of composite amplifiers with the topology described by John D. Yewen's article in Electronics & Wireless World, February 1987 and promised we can do even better.

One of the issues with Yewen's topology:

is that R1 R2 (in the schematic above) attenuate the signal amplified by U1, which causes U1 to work extra hard, or, more precisely, work with a higher input signal. As was discussed previously on this blog, this affects the linearity of U1's input stage and adds distortion that cannot be corrected by feedback.

One way to address this issue is to use a better opamp as U1, but it is much easier to move the divider to U1's input:

R1 R2 should be large compared to Ri to avoid an unwanted noise gain increase and a loop gain reduction (see the discussion in my previous post), but otherwise this works exactly the same as Yewen's composite, only with lower distortion.

Naturally, this approach also works with frequency dependent dividers:

High Precision Composite Op-Amps, Part 4 - A Practical Composite Chipamp with LM1875

This post is a part of the series on audio amplifier feedback. The contents of the series can be found here.

In my previous post on this topic, I discussed the role of the voltage divider in John D. Yewen's composite op-amps (see his article in Electronics & Wireless World, February 1987) and improving the composite's loop gain at audio frequencies by making the divider frequency dependent.

Towards the end of the previous post, I promised that this approach works in hardware, too, so here are two practical examples.

The first is a plain Yewen composite with two dissimilar opamps - an OPA134 and an LM1875:

The divider (R4R5) attenuates the output of the OPA134 by 33/(2200+33)≅-36dB, which together with the opamp's GBW of 8MHz places the zero (see my previous post for an explanation) at about 130kHz. It is kind of low, but in testing, placing the zero at a higher frequency made for poor clipping performance. With such a divider, the OPA134 adds about 16dB of loop gain at 20kHz (more at lower frequencies), and this composite produces 0.003% THD at 1kHz, 20W into 8ohm, or about 1/6 of the distortion of a standalone LM1875.

The second example is a composite with the same opamps and a frequency dependent voltage divider C4C5R10:

The improved divider adds a pole at 2kHz and a zero at 150kHz, increasing the loop gain by another 16dB at 20kHz while maintaining stability and clipping similar to that of the first composite. With a careful PCB layout, this composite should be able to deliver 0.001% of THD at 1kHz, 20W into 8ohm.

Note that for both versions, the Zobel network (R6C2 and R11C6, respectively) with the values shown is required for stability.

Can we make the composite still better? Yes we can! Stay tuned...

High Precision Composite Op-Amps, Part 3 - More Loop Gain

This post is a part of the series on audio amplifier feedback. The contents of the series can be found here.

As discussed in my previous post on this topic, the resistive voltage divider in John D. Yewen's composite amplifier (see his article "High-precision composite op-amps" in Electronics & Wireless World, February 1987):

adds a zero to the loop gain, which helps to achieve stability at the expense of the loop gain:

For audio applications, it is desirable to maximize the loop gain, at least in the audio band, but preserve the phase margin. One way to keep that zero and maximize the loop gain at audio frequencies is to make the voltage divider frequency dependent, for example:

Adding an inductor in parallel to R3 adds a pole-zero pair (disregarding the inductor's own series resistance, the pole is at $F_p={1 \over {2 \pi}} {{R_3 || R_4} \over L_1}$, the zero at $F_z={1 \over {2 \pi}} {R_3 \over L_1}$). With the values shown, we get about 12dB of extra loop gain at 20kHz with the same phase margin as without the inductor:

 A 22mH inductor may not be very practical, but a similar effect can be achieved with a resistive-capacitive divider, for example:

Here, the pole is at $F_p={1 \over {2 \pi R_5 (C_1 + C_2)}}$, the zero at $F_z={1 \over {2 \pi R_5 C_1}}$. With the values shown, the loop gain is about the same as with the inductor above:

 

Not bad for one additional passive component. It works in hardware, too - I will show a practical example in my next post.